数理モデルでつなげる脳の仕組み vol.5
大切な情報をどうやって伝えているのか
理論的なコンセプトから研究を始めて学べることは、たくさんあります。冒頭にお話ししたように、脳の学習も生物の進化も、時間スケールは違うものの、環境への適応プロセスであるという点は共通しています。
進化の場合には、子孫をより多く残せる遺伝子を持った種が残り、そうでない種は少なくなっていきます。実際の進化を抽象化した遺伝子アルゴリズムでは、このプロセスを「生存率の最適化」と考えます。そう考えることで、環境が変化したあと、よりその環境に適合し生存率の高い種が進化し繁栄する様子を説明することができるのです。
脳の学習もやはり環境への適応であれば、同じようなアルゴリズムでその過程を説明することができるかもしれません。ニューロンの場合には、報酬の最大化(快を増やして不快を減らす)に関する理論がありますが、脳の学習は、報酬に関連したものばかりではありません。とくに脳の構造が著しく成長する幼年期には、明確な報酬信号がなくても学習が進みます。
そこで考えたのが、ニューロンの情報伝達効率の最大化です。もしニューロンが大切な情報をより効率よく次のニューロンに伝えるためにシナプス強度を変化させたら、どのようなシナプス可塑性の法則が導き出せるでしょうか?数式を使って計算してみました。
おもしろいことに、情報伝達効率の最大化から理論的に見出されたシナプス可塑性は、脳で実験的に観測されているヘブ則と非常に近いものでした。それでは、このような学習法則に従ってシナプス強度が変化したらどうなるだろうかと考えました。もし出力するニューロンと入力するニューロンが1対1なら、おもしろい結果は出ません。情報伝達効率を高めるためには、単に、入力情報をすべてコピーして出力するだけだからです。
しかし、出力ニューロン1つに対して、入力ニューロンが1万から10万個もある実際の状況では、入力ニューロンの情報をすべて伝えることは不可能です。そうすると、出力ニューロンは必然的に情報を取捨選択することが必要になります。つまり、入力情報の特徴を抽出して表現するようになるのです。具体的には、バラバラに発火するニューロン集団からのシナプス強度は弱めて、一番まとまりをもって発火するニューロン集団からのシナプス強度を強化します(図8)。もっとも正確に伝えることができる情報を選りすぐって伝達するよう学習が進んだのです。
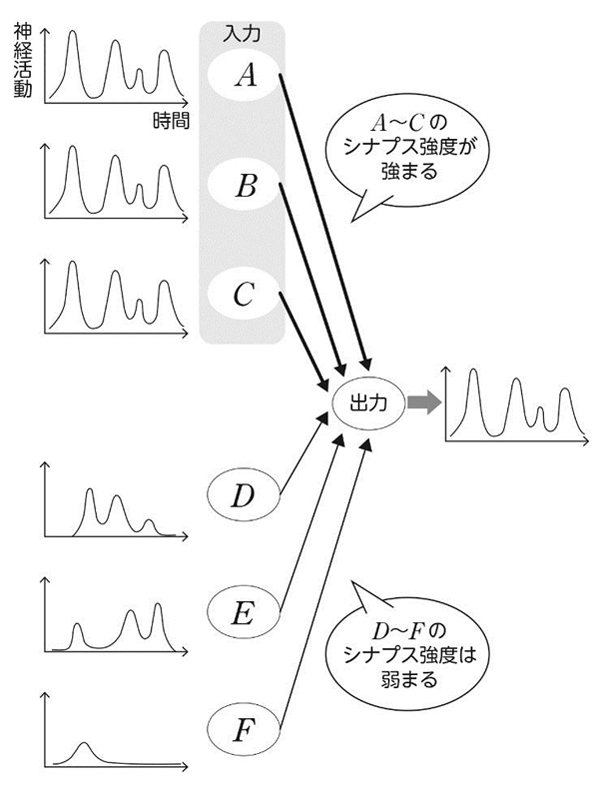
入力ニューロンA~Cは同じパターンの神経活動をしていて、まとまった情報を入力している。
出力ニューロンはこの集団のシナプス強度を強めて、情報を伝えるようになる。D~Fのシナプス強度は弱まる。
そういう状況で、感覚ニューロンの集団から入力を受け取る出力ニューロンの学習を考えてみます。この「情報伝達効率最大化」の学習則を当てはめてみると、たくさんの感覚ニューロンの中から、同時に発火する頻度のいちばん高い集団を選択し、それに応答するようなニューロンが、自発的に現れたのです。
たとえば、学習の過程で入力するものが画像情報のとき、同じパターンの画像が繰り返し提示されたら、その画像のパターンに選択的に応答するニューロンが現れます。また、音情報で学習させるとき、特定の声を繰り返し聞くと、その声の周波数構造の関係を統合するニューロンが現れるのです。ここでのポイントは、あくまで各ニューロンでは情報伝達効率の最適化というルールは変わらず、入力された情報(環境)に応じてニューロンの選択性が自発的に生まれるというシミュレーションの結果が得られたことです。
大勢の中から知人の声を聞き分けるアルゴリズム
私たちは、このような神経情報の最適化というアプローチからも研究を進めています。
それは、複数の出力ニューロンの伝える情報伝達効率を最大化するようにする、ということです。ヒントになったのは人工知能分野の研究です。20年ほど前の研究ですが、複数のニューロンからの出力を考え、それらの情報量の総和が増えるような学習則を与えたとき、この神経回路は全体でどんな情報を表現するようになるかを探った研究があるのです。
結果としては、おもしろいことに、独立成分分析のできる神経回路ができました。独立成分分析を簡単に説明すると、未知の混ざりあった信号を一つ一つ選り分けられる数学的な手法の一つです。たとえば、何人かで会話している音声データがあったとき、そのアルゴリズムを使うと、それぞれの声をすべて分離してくれるのです。
パーティー会場でたくさんの人が周りで話している状況を考えてください。そのような状況でも私たちは特定の相手の声をその他から分離して聞き分けることができます(図9)。

「カクテルパーティ効果」とも呼ばれる。実際の脳がどのように音を聞き分けているのか、その仕組みはまだ分かっていない。
このアルゴリズムは、工学的にはすごいことです。なにせ、原理的には、どんなノイズもカットして、信号をクリアにできるということなのですから。実際にこの方式は、潜水艦のソナー(水中の物体を捜索する装置)などにも実用化されています。
おもしろい応用例だと、ビデオカメラで顔を撮影すると心拍数が測れる、なんてこともできます。画像に含まれるさまざまな揺らぎを分離して、心拍数に相当する振動だけを抽出するわけです。
しかし、本物の脳に、このアルゴリズムが実装されているかは疑問でした。なぜなら、ニューロンが行うには難しそうな学習則だからです。
このアルゴリズムをニューロンに実装するには、離れた場所にあるシナプス同士が、お互いの情報を共有する必要があります。しかし、そういう知見は、本物のニューロンでは見つかっていません。工学的には、とても使える学習則なのですが、神経回路で実装するのは難しそうなモデルなのです。
それを近似してニューロンでも実装できるようにしたアルゴリズムもありますが、入力の特性をあらかじめ仮定した前処理が必要であったり、性能が悪かったりして一長一短でした。
しかし私たちは、そこを克服して、ニューロンに実装できるような高性能の学習則を作りました(図10)。そのアルゴリズムを、現在開発が進むニューラルネットワークチップに使えば、膨大なデータを並列計算によって高速に独立成分に分離できると考えています。
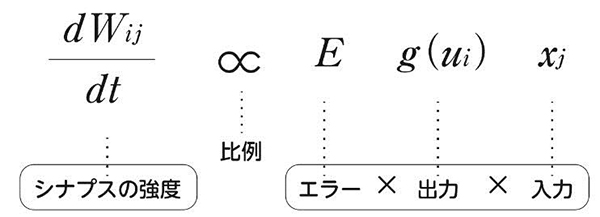
式中のdWij/dtはシナプス強度の時間的変化、gは非線形関数。
たくさんの「解」があることに意味がある
入力と結果としての出力は同じであっても、内部のアルゴリズムに違いのあることは、一般的にありうることです。現実の世界では、たった一つのアルゴリズム(解)に定まることのほうが少ないでしょうし、たくさんの解があることのほうが、生物学的には重要な気がしています。
神経回路と機能の対応性について、ほぼ同じ機能を有する神経回路でも実装の仕方は複数あって、それが大切なのだという意味のことを提唱している研究者もいます。たとえば、いったん環境が変わって、そこからまた元の環境に戻ると、神経回路は元々の環境に再度適応するわけですが、そのときに実装された神経回路の詳細は、環境が変化する前とは異なっているということがよくあるのです。そうした機能のレパートリーのようなものが、たくさんあるということです。
それこそ、進化は適応の歴史です。環境が変わったときに適応するため、そして特定の生物要素がうまく働かない場合にも備えて、さまざまな解の組み合わせをあらかじめ持っているということが大切な意味を持っていると思うのです。
物理の理論に、最大エントロピー原理というものがあります。いくつか言い方はあるのですが、ここでは「エネルギーが一定という観測だけが与えられた場合、状態としては、その制約条件の下でもっとも多様な組み合わせを考えるのが適当である」と表現しましょう。これを生物学的に言いなおすと「進化が淘汰圧のみで決まるのであれば、生き残るという制約条件の下でもっとも多様な神経回路パターンを持つ種が観測される」ということです。生き残れるパターンのうち、よりレパートリーの多い、つまり多様性が保持されている種が進化の果てに生き残っているのだとすれば、それは当然、脳にも当てはまるのではないでしょうか。
個人的には、脳から学べることは多いと思っていますが、とくに脳だけにこだわっているわけではありません。極端な話、コンピュータウイルスのように、ネット上で進化していく存在からも学べるものがあるかもしれません。
冒頭にも言いましたが、進化と学習のプロセスは、すごく近いところがあると思います。したがって、外界に素早く適応していけるような進化や学習のルールがどういうものなのかを追究していくことが、私にとって一番おもしろいのです。複雑な現象の背後にある本質を見抜くことで、環境から学んで知能を発達させていくルールの核の部分を見つけたいですね。
著者:豊泉太郎 神経適応理論研究チーム チームリーダー
出典:講談社ブルーバックス
つながる脳科学(数理モデルでつなげる脳の仕組み) もくじ
- 数理モデルでつなげる脳の仕組み vol.1
- 数理モデルでつなげる脳の仕組み vol.2
- 数理モデルでつなげる脳の仕組み vol.3
- 数理モデルでつなげる脳の仕組み vol.4
- 数理モデルでつなげる脳の仕組み vol.5