数理モデルでつなげる脳の仕組み　vol.4

ディープラーニングの元になった理論

私が学生になるずっと前から、「パーセプトロン」や「ネオコグニトロン」のような、脳の働く仕組みをコンピュータ上で模倣するニューラルネットワーク（神経回路網）のモデルがありました。そんなに古いものだと思いきや、最近は、それらのニューラルネットワークを改良した「ディープラーニング（深層学習）」がブームになっています。

ディープラーニングは、将棋や囲碁の人工知能（AI）から車の自動運転にまで応用されているので、耳にしたことのある読者もいるかもしれません。

パーセプトロンは、簡単な構造で表現されているのに多様な学習ができることで有名になりました。パーセプトロンの基本設計は、外部からの信号が与えられる入力層（感覚層）、その入力層の情報を統合して入力の特徴を抽出する中間層（連合層）、そして最終的な出力を生成する出力層（反応層）の３層に分けられます（図７）。

図7 パーセプトロンの基本設計
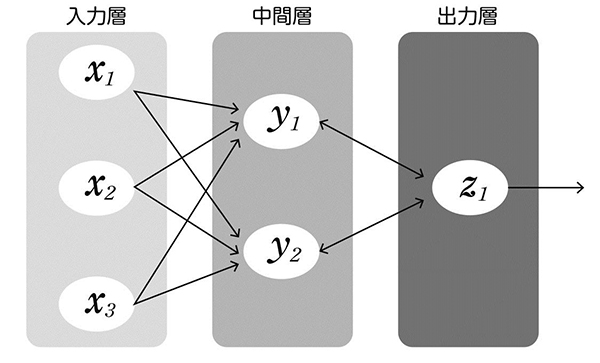
入力層で受け取った情報が中間層で変換され、出力層が解を出す、という3層に分けられる。

各層にはニューロンに相当する素子があり、前の層のニューロンからの信号を足し合わせ、それを、非線形な関数で変換して次の層に伝えます。ニューロン数を十分に用意すれば、理論的にはどんな入出力関係でも表現できることが数学的に証明できます。その意味でパーセプトロンは「万能機械」と呼ばれています。しかし実際には、そのような最適な表現を獲得することは困難でした。可能性はあっても実際に学習することができなかったのです。

一方、文字認識や物体認識に関して、脳の視覚野の性質を模倣したニューラルネットワークも考案され始めます。

ネオコグニトロンや「畳み込みニューラルネットワーク」と呼ばれるモデルがそうで、文字や物体の形が多少変化しても、脳が同じものとして認識するための仕組みを、ニューラルネットワークにも実装しました。

脳の視覚野には「単純細胞」と「複雑細胞」という２種類のニューロンが存在します。まず、単純細胞が視野の中の特徴的パターン、たとえば一定の傾きを持つ線分を検出します。しかし、線分の位置が少しずれると、単純細胞はすぐに発火しなくなってしまいます。

そこで複雑細胞は、ある一定の傾きを持つ線分に反応する単純細胞から、担当する位置を問わず、広く入力を集めます。そして、その中に発火している単純細胞があれば、自らも発火します。こうすることで複雑細胞は、一定の傾きを持つ線分に対して、その位置によらず応答できるようになるのです。このような単純細胞と複雑細胞の情報処理を多数の中間層を使って繰り返すことで、線分以外のさまざまな特徴パターンに対しても多少のズレを問わず発火できるようにニューロン集団が学習します。

ディープラーニングの謎

今流行りのディープラーニングも、基本的な設計思想に関して言えば、これらのたくさんの中間層を使うモデルとよく似ています。しかし、当時とは決定的に違うのが計算・情報技術の進歩です。元々のアイデアが提唱された1980年代と比べると、コンピュータの計算力は、ものすごく上がっていますよね。そして、ディープラーニングでは、その計算力を背景にして大量の訓練データを扱います。もちろん、コンピュータの計算力が圧倒的に大きくなったことにも応じているのですが、ありとあらゆるデータがクラウド上にデータベース化されている時代ですから、昔とはデータの量も種類も比べることが無意味なほど膨大です。

昔ながらの３層パーセプトロンも、理論的な学習可能性からすると、万能機械だということを説明しました。では、なぜ３層パーセプトロンだと学習がうまくいかなくて、ディープラーニングだとうまくいくのかというと、じつはまだ確かな理由は分かっていません。乱暴な言い方になりますが、直感的にやってみたらうまくいったという話だと思っています。そして現在、多くの研究者がその理由を探求しています。

たとえば、ディープラーニングを使って、クラシカルなビデオゲームを学習させると、人間よりもプレイの上手な機械を作ることができます。そういうところは、本当に興味深い領域だと思っています。アーケードゲームのようなものだと、機械はスコアと画面を認識して操作するのですが、人間よりもハイスコアを出せるようになるだけでなく、試行錯誤によってさまざまな戦略をあみだします。

おもしろいのは、過去の記憶に相当するデータを学習に利用する点です。単純に、今のゲームの状況が良いか悪いかを判断して学習を進めるだけではなく、過去のゲーム画面をプールしておいて、たまに再生させては学習して、今のプレイに反映させるのです。人間が、あのときこうだったな、などと思い出す感じに近いですね。人工的に組み込んだプロセスではありますが、脳の海馬領域が記憶を状況に応じて再生して定着させる仕組みを模倣したものであり、脳の学習からヒントを得て成功した例の一つです。

脳の中のニューロンを模した計算素子、視覚野で発見された単純細胞と複雑細胞の階層構造、そして海馬の記憶定着メカニズムを組み込んで、人工知能は新しい分野で人間に追いつき、追い越しつつあります。そこから、生物学的制約条件にとらわれない工学的実装がパワフルであることが分かると同時に、脳から学ぶ計算原理の奥深さも感じます。

人間はAIに負けるのか？―人工知能と脳の学習とのギャップ

ただし、神経科学としてディープラーニングを見たときの大きなミステリーの一つは、「誤差逆伝搬法」と呼ばれる学習法則が人工的であることです。

ディープラーニングで、最終的な出力を改善するために、出力層へとつながるシナプス強度をどう調節したらよいかは簡単に計算できます。つまり、出力をもっと増やしたければ（もしくは減らしたければ）、現在たくさん発火しているニューロンから出力ニューロンへとつながるシナプス強度を強めれば（弱めれば）良いのです。

しかし、入力層付近のシナプス強度をどう調節したら最終的な出力が改善されるか、という計算は少し複雑です。入力層付近のニューロンの活動パターンを網羅的に試してみて、どのパターンがもっとも出力を改善するかを調べていたら、膨大な時間がかかってしまいます。そこで、期待される出力（教師信号）と実際の出力層との誤差を、発火の信号とは逆方向に、出力側から入力層側へ向かって伝えていくのです。これを誤差逆伝搬法といいます。

このように誤差を逆伝搬することで、出力層の誤差が各層のどのような発火活動に対応するかが分かり、シナプス強度の調節の仕方も計算できます。これは工学的には大変有用な手法ですが、脳でそのような仕組みは見つかっていません。もし、生物学的な神経回路で誤差の逆伝搬が見つかれば、理論予測が検証されたということできわめて画期的なことだと思うのですが、現状では、多くの脳研究者は、脳が誤差逆伝搬を用いているとは思っておらず、ディープラーニングによる学習と脳の学習は、系統の違うものだと考え、その学習方式を研究しています。

チェスに関しては20年前に人間が人工知能に敗れました。今では囲碁でもそうですが、狭い分野に限れば、人間の知能は機械に超えられています。これはもちろん、「知能」の定義によります。ゲームのように、ルールが決まっていて、有限の選択肢から状況を進めて行くような課題に関しては、早晩、人間は追いつけなくなると思います。

一方で、現在の人工知能はまだ比較的狭い範囲の課題に特化していて、その課題に関して人間よりはるかに多くの訓練データを使って学習しています。おそらく、もっと少数の訓練データで勝負をしたら、人間に軍配が上がるでしょう。その理由は、人間がもっと広範囲の課題をこなしていて、ある課題から学んだ知識を、それとは一見別と思われる課題に生かしているからかもしれません。そう考えると、今のところ、人間のほうが社会に関する基礎知識（常識）があると言えるのかもしれません。

著者：豊泉太郎　神経適応理論研究チーム　チームリーダー

出典：講談社ブルーバックス

つながる脳科学（数理モデルでつなげる脳の仕組み）　もくじ