数理モデルでつなげる脳の仕組み　vol.3

「足し算」ではなく「掛け算」？

しかし、このような時間スケールの異なる２種類の可塑性を従来のモデルに入れてシミュレーションすると、神経回路は、安定化するどころか、逆に不安定になることが分かりました。ヘブ則と恒常性の可塑性が綱引きをして、状態の釣り合ったところで安定化することが期待されていたのですが、二つの可塑性の時間スケールが違うと、シナプス強度が揺れ動いて振動してしまうのです。まるで、シャワーの温度を変えたいときに、ぬるくて温度を上げると熱くなりすぎ、かといって温度を下げるとぬるくなりすぎるという状況と似ています。温度が変わるまでに遅れがあると、ちょうどよいところを見つけるのが難しいというイメージです。

したがって、この二つの可塑性の組み合わせ方に問題があるのだと考えました。従来のモデルは、「綱引き」と言われるように、二つの可塑性の釣り合いを考えて、ヘブ則と恒常性の可塑性の効果を足し合わせてゼロになるようにシナプス強度を動かすという、「足し算」を使ったモデルでした。それだと、一方の可塑性を他方が邪魔し、競合している状態になります。したがって、二つの時間スケールが大きく違うとちょうどよい折衷点を見つけられません。

ところが、「掛け算」でモデルを作ると、システムとして安定することが見出されたのです。今までの学習則では、お互いの効果を打ち消してしまうことが起こったのですが、新しいモデルでは、２種類の可塑性がそれぞれ別にあるシナプス強度の調整因子に独立に働き、それらの変数の掛け算で最終的なシナプス強度が決まると考えています。このモデルだと、２種類の可塑性の効果が直接打ち消しあうことはありません。したがって、可塑性の生じるタイムスケールが違っても二つの間に競合は起こらず、うまく学習できるということが分かりました。

それでは、この理論の中身は、どのような生物学的な現象に対応するのでしょうか。そもそも「シナプス強度」と一口にいっても、その中には、さまざまな内容の分子的な現象が含まれています。つまり、２種類の可塑性がシナプス強度を調整する因子とは具体的に何か？ということです。

たとえばシナプスは、大きくシナプス前部とシナプス後部の二つに、構造が分かれます。シナプス前部とシナプス後部の間は密着しているわけではなく、微小な隙間（シナプス間隙）があります（『つながる脳科学』第1章52頁コラムを参照）。シナプスにおける情報伝達は基本的に一方通行で、シナプス前部からシナプス後部に向けて、シナプス間隙に神経伝達物質が放出されます。放出された神経伝達物質は、シナプス後部にある受容体（レセプター）に受け取られて、シナプス後部側のニューロンを興奮させたり、抑制したりするのです。

このとき、シナプス前部側の神経伝達物質を放出する頻度と、シナプス後部側の感度を掛け算したものが、シナプス強度と考えられます。シナプス後部に注目してみると、個々のレセプターの影響の大きさとレセプターの数の掛け算がシナプス後部側の感度に相当します。つまり、いくつものステップの掛け算が、最終的なシナプス強度として表されるわけです。

恒常性の可塑性とヘブ則が、それぞれ実際の脳内の分子メカニズムとどう関係しているのかは、まだ完全には分かっていません。今の段階で予想しているのは、恒常性の可塑性がシナプス後部のレセプターの密度を制御し、ヘブ則がシナプス後部の体積を制御し、それらの掛け算、つまりシナプス後部にあるレセプターの数でシナプス強度が決まるという可能性です（図６）。

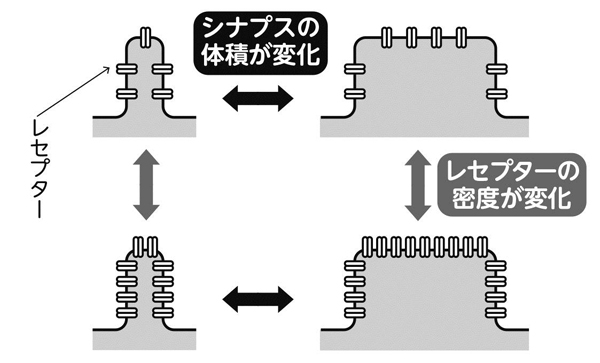
図6 シナプス強度はどうやって決まる?
シナプス後部に存在するレセプターの密度と、シナプス自体の体積の「掛け算」でシナプス強度が決まっているのかもしれない。

もしこの理論が正しければ、２種類の可塑性の時間スケールが違っても、シナプス結合が不安定になって振動する現象は起きません。そしてこのモデルから、視覚野におけるシナプス強度に関して、いくつかの予測が立てられて、一部は実験的に確認できています。

まだ完全なモデルではありませんが、いくつかの問題をクリアできれば、将来的にさまざまな記憶の獲得や保持をモデルで再現することが期待できます。そうなれば、連想や古典的な強化学習（ベルが鳴ったらエサがもらえる、電話の声を聞いて相手の顔が思い浮かぶなど）のようなさまざまな学習を、より生物学的な神経回路モデルを使ってシミュレーションできるようになり、かなり脳の理解が進むと思います。

理論屋と実験屋

私はいわゆる「理論屋」なので、常に、思いついたさまざまなアイデアを頭の中で次々に試していくというのが「研究する」ということになります。興味の範囲内で試せることが100も200もあるので、書きなぐっては、くしゃくしゃと丸めてポイみたいなことを延々と繰り返していて、たまに当たりがある感じです。アイデアは次々と思いつくのですが、大抵はうまくいきません。「実験屋」の研究者も、90％は失敗だと言いますから、そのあたりは似たようなものかもしれませんけれど。

実験から研究を進めることに比べて、理論から脳の仕組みを解明することには、いくつかのメリットがあります。一つは、メソッドに縛られないことです。実験動物にすら縛られません。たとえば人間も対象にできますし、サルでも、もちろんマウスやラット、魚類でも、理論なら広い意味で考えられます。

もう一つは、実験が導き出す結論とは異なる、別の確信にたどり着けることです。実験では、遺伝子などの分子メカニズムのように、実験的に「操作できる」ものを重要視すると思います。それに対して、理論研究では、包括的なコンセプトに関して話せるのです。

これから先、「ビッグデータ」という名前のとおりどんどんデータが増えていくと、それを解析する機械学習のアルゴリズムの設計も含めて、数理を使って見通しを立てるほうが、研究を進めるうえでよいだろうと思います。数理とは、広い意味で、数学を使って世の中を考えることです。実験屋が膨大なデータに埋もれている、などと言うつもりはありません。ただ理論屋は、事の詳細にかかわらず、全体の性質が抽出されている何かを探すプロセスを専門にしているといってもいいでしょう。

そういう意味では、理論の研究で重要なことは、「無駄を省く」ことだろうと思います。ようするに、複雑な生物を理解するために、さまざまな要素をばっさりと切り捨てていくわけです。物理学の世界では、ものごとをできるだけシンプルにするということが、ニュートン以来の伝統です。たとえば、物体の運動を解析するときは摩擦なり何なりあるわけですが、そういう要素を無視しても、りんごが落下したり、星が回っている様子を説明できます。最近であれば、機械学習のアルゴリズムのデザインも含めて、複雑なものごとの骨格を見抜くためのツールが数理なのだ、というとイメージしてもらえるでしょうか。

著者：豊泉太郎　神経適応理論研究チーム　チームリーダー

出典：講談社ブルーバックス

つながる脳科学（数理モデルでつなげる脳の仕組み）　もくじ